Active Subspaces

Sometimes, the behavior of an \(N\)-dimensional model \(f\) can be explained best by a linear reparameterization of its inputs variables, i.e. we can write \(f(\mathbf{x}) = g(\mathbf{y}) = g(\mathbf{M} \cdot \mathbf{x})\) where \(\mathbf{M}\) has size \(M \times N\) and \(M < N\). When this happens, we say that \(f\) admits an \(M\)-dimensional active subspace with basis given by \(\mathbf{M}\)’s rows. Those basis vectors are the main directions of variance of the function \(f\).

The main directions are the eigenvectors of the matrix

\(\mathbb{E}[\nabla f^T \cdot \nabla f] = \begin{pmatrix} \mathbb{E}[f_{x_1} \cdot f_{x_1}] & \dots & \mathbb{E}[f_{x_1} \cdot f_{x_N}] \\ \dots & \dots & \dots \\ \mathbb{E}[f_{x_N} \cdot f_{x_1}] & \dots & \mathbb{E}[f_{x_N} \cdot f_{x_N}] \end{pmatrix}\)

whereas the eigenvalues reveal the subspace’s dimensionality –that is, a large gap between the \(M\)-th and \((M+1)\)-th eigenvalue indicates that an \(M\)-dimensional active subspace is present.

The necessary expected values are easy to compute from a tensor decomposition: they are just dot products between tensors. We will show a small demonstration of that in this notebook using a 4D function.

Reference: see e.g. “Discovering an Active Subspace in a Single-Diode Solar Cell Model”, P. Constantine et al. (2015).

import tntorch as tn
import torch

def f(X):
    return X[:, 0] * X[:, 1] + X[:, 2]

ticks = 64
P = 100
N = 4

X = torch.rand((P, N))
X *= (ticks-1)
X = torch.round(X)
y = f(X)

We will fit this function f using a low-degree expansion in terms of Legendre polynomials.

t = tn.rand(shape=[ticks]*N, ranks_tt=2, ranks_tucker=2, requires_grad=True)
t.set_factors('legendre')

def loss(t):
    return torch.norm(t[X].torch()-y) / torch.norm(y)
tn.optimize(t, loss)

iter: 0      | loss:   0.999513 | total time:    0.0020
iter: 500    | loss:   0.977497 | total time:    0.8296
iter: 1000   | loss:   0.763221 | total time:    1.6445
iter: 1500   | loss:   0.044802 | total time:    2.5523
iter: 2000   | loss:   0.008546 | total time:    3.4807
iter: 2266   | loss:   0.008208 | total time:    3.9928 <- converged (tol=0.0001)

eigvals, eigvecs = tn.active_subspace(t)

import matplotlib.pyplot as plt
%matplotlib inline
plt.figure()
plt.bar(range(N), eigvals.detach().numpy())
plt.title('Eigenvalues')
plt.xlabel('Component')
plt.ylabel('Magnitude')
plt.show()

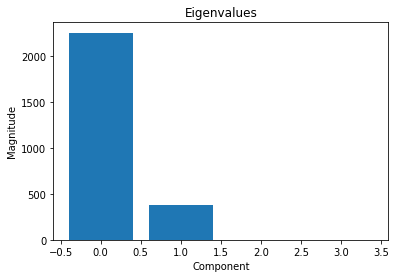
In view of those eigenvalues, we can conclude that the learned model can be written (almost) perfectly in terms of 2 linearly reparameterized variables.